Муниципальное бюджетное общеобразовательное учреждение
«Лицей № 48»
города Калуги

http://terepec48.ru

Сумма углов треугольника.

Смирнова И. Н., учитель математики.
Информационный проспект открытого урока.

1. Мотивация изучения теоремы.
2. Раскрытие содержания теоремы в ходе математического эксперимента с использованием учебно-методического комплекта «Живая математика».
3. Мотивация необходимости доказательства теоремы.
4. Работа над структурой теоремы.
5. Поиск доказательства теоремы.
6. Доказательство теоремы.
7. Закрепление формулировки теоремы и ее доказательства.
8. Применение теоремы.

Урок по геометрии в 7 классе
по учебнику «Геометрия 7-9»
на тему: «Сумма углов треугольника».

1. Актуализация знаний.
   1. Мобилизующее начало урока.
   2. Постановка проблемной задачи с целью мотивации изучения нового ма-териала.
   3. Постановка учебной задачи.
2. Формирование новых знаний и способов действий.
   1. Практическая работа «Сумма углов треугольника».
   2. Доказательство теоремы о сумме углов треугольника.
3. Применение знаний, формирование умений и навыков.
   1. Решение проблемной задачи.
   2. Решение задач по готовым чертежам.
   3. Подведение итогов урока.
   4. Постановка домашнего задания.

Ход урока.

1. Актуализация знаний.
   1. Мобилизующее начало урока.
      После приветствия учащимся сообщается план работы на уроке:
      • Изучение нового материала.
      • Итог урока.
      • Домашнее задание.
   2. Постановка проблемной задачи с целью мотивации изучения нового материала.
      Учитель: На предыдущем уроке мы с вами написали контрольную работу и тем самым закончили изучение главы учебника, которая называлась «Параллельные прямые». Но на этом курс геометрии в 7 классе не заканчивается.
      Сегодня на уроке мы приступаем к изучению последней главы нашего учебника.
      Но прежде чем начать ее изучение, давайте вернемся к началу и вспомним что изучает наука геометрия?
      Ученик: Геометрия – наука о свойствах геометрических фигур.
      Учитель: Ответьте на следующий вопрос. Изучению какой геометрической фигуры мы уделяли больше всего внимания в 7 классе?
      Ученик: Треугольник.
      Учитель: Как вы считаете, почему именно с треугольника мы начали изучение гео-метрии в 7 классе?
      Ученик: Треугольник – самая простая замкнутая прямолинейная фигура, свойства ко-торой человек узнал еще в глубокой древности, так как эта фигура всегда имела ши-рокое применение в практической жизни (строительстве и земледелии), любой мно-гоугольник можно диагоналями разделить на треугольники.
      Учитель: Действительно, хотя треугольник и самый простой по виду из многоуголь-ников, но по количеству свойств он опережает многие более сложные фигуры.
      Вспомните, что важного о треугольнике мы уже узнали в 7 классе?
      Ученик: Признаки равенства треугольников, виды треугольников, новые элементы треугольника — биссектриса, медиана и высота.
      Учитель: Действительно, мы умеем строить треугольники, умеем их сравнивать, зна-ем названия его элементов, но, к сожалению, мы пока не умеем находить элементы треугольников: стороны и углы. Наша цель – научиться это делать.
      Начнем с нахождения углов. Рассмотрим такую задачу.
      

      Задача

      ---

      Дано: Треугольник ABC,
      угол A = 50°,
      угол B = 100°,
      Найти: угол C.

      Учитель: Как вы считаете, можно ли решить эту задачу?
      Ученик: Да.
      Учитель: Сколько решений имеет эта задача?
      Ученик: Одно.
      Учитель: При каком условии задача будет иметь единственное решение?
      Ученик: Задача имеет единственное решение, если сумма углов любого треугольника величина постоянная.
      Учитель: То есть, для решения задачи надо знать величину суммы углов треугольника.
      
   3. Постановка учебной задачи. Учитель: Итак, ставлю перед вами учебную задачу: в ходе урока вы должны будете определить, чему равна сумма углов треугольника, и научиться решать задачи, связанные с нахождением углов треугольника.
      
      Приступаем к выполнению этих задач. На первом этапе урока в ходе практической работы вы должны будете выдвинуть гипотезу о величине суммы углов произвольного треугольника.

   План урока:

   ---

   1. Экспериментальным путем установить и выдвинуть гипотезу о сумме углов любого треугольника.
   2. Доказать это предположение.
   3. Закрепить установленный факт.
   
   

   Почему важен эксперимент

   ---

   • Очень часто ученые сначала экспериментальным путем устанавливают важные факты, а потом доказывают их при помощи логических рассуждений.
   • Это происходит в химии, физике и геометрии.

   
2. Формирование новых знаний и способов действий.
   1. Практическая работа «Сумма углов треугольника».
      Учащиеся садятся за компьютеры и им раздаются карточки с планом практической работы.

      Практическая работа по теме «Сумма углов треугольника» (образец карточки)

      Распечатать карточку
      

      Класс

      _________________

      Фамилия, имя

      ___________________________

      Этапы практической работы	Результаты практической работы
      Запустите программу «Живая математика».
      Постройте произвольный треугольник.
      Измерьте все углы данного треугольника.
      Вычислите сумму углов построенного треугольника.
      Подвигайте вершины треугольника таким образом, чтобы вид треугольника изменился. Изменилась ли при этом движении сумма углов треугольника?
      Подумайте, зависит ли сумма углов треугольника от его вида?
      Выскажите гипотезу о том, чему равна сумма углов треугольника.

      Учащиеся сдают результаты практической работы и садятся за парты.
      После обсуждения результатов практической работы выдвигается гипотеза о том, что сумма углов треугольника равна 180°.
      Учитель: Почему мы пока не можем утверждать, что сумма углов абсолютно любого треугольника равна 180°.
      Ученик: Нельзя выполнить ни абсолютно точных построений, ни произвести абсолютно точного измерения, даже на компьютере.
      Утверждение, что сумма углов треугольника равна 180°, относится только к рассмотренным нами треугольникам. Мы ничего не можем сказать о других треугольниках, так как их углы мы не измеряли.
      Учитель: Правильнее было бы сказать: рассмотренные нами треугольники имеют сумму углов приблизительно равную 180°. Чтобы убедиться в том, что сумма углов треугольника точно равна 180° и при том для любых треугольников, нам надо еще провести соответствующие рассуждения, то есть доказать справедливость утверждения, подсказанного нам опытом.
      
   2. Доказательство теоремы о сумме углов треугольника.
      Учащиеся открывают тетради и записывают тему урока «Сумма углов треугольника».

      Работа над структурой теоремы.

      Чтобы сформулировать теорему, ответьте на следующие вопросы:
      • Какие треугольники использовались в процессе проведения измерений?
      • Что входит в условие теоремы (что дано)?
      • Что мы обнаружили при измерении?
      • В чем состоит заключение теоремы (что надо доказать)?
      • Попробуйте сформулировать теорему о сумме углов треугольника.

      Построение чертежа и краткая запись теоремы

      На этом этапе учащимся предлагается сделать чертеж и записать, что дано и что требуется доказать.

      Построение чертежа и краткая запись теоремы.

      ---

      Дано: Треугольник ABC.
      Доказать:
      டA + டB + டC = 180°.

      Поиск доказательства теоремы

      При поиске доказательства следует попытаться развернуть условие или заключение теоремы. В теореме о сумме углов треугольника попытки развернуть условие безнадежны, поэтому разумно заняться с учениками развертыванием заключения.
      Учитель: В каких утверждениях говорится об углах, сумма величин которых равна 180°.
      Ученик: Если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 180°.
      Сумма смежных углов равна 180°.
      Учитель: Попробуем для доказательства использовать первое утверждение. В связи с этим необходимо построить две параллельные прямые и секущую, но необходимо это сделать так, чтобы наибольшее количество углов треугольника стали внутренними или входили в них. Как можно этого добиться?
      

      Поиск доказательства теоремы.

      ---

      
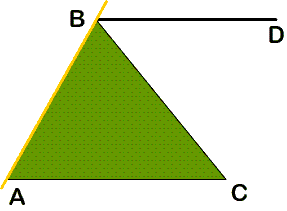      Ученик: Провести через одну из вершин треугольника прямую параллельную другой стороне, тогда боковая сторона будет являться секущей. Например, через вершину В.
      Учитель: Назовите образовавшиеся при этих прямых и секущей внутренние односторонние углы.
      Ученик: Углы DBA и ВАС.
      Учитель: Сумма каких углов будет равна 180°?
      Ученик: டDBA и டBAC.
      Учитель: Что можно сказать о величине угла ABD?
      Ученик: Его величина равна сумме величин углов ABC и СВК.
      Учитель: Какого утверждения нам не хватает, чтобы доказать теорему?
      Ученик: டDBC = டACB.
      Учитель: Какие это углы?
      Ученик: Внутренние накрест лежащие.
      Учитель: На основании чего мы можем утверждать, что они равны?
      Ученик: По свойству внутренних накрест лежащих углов при параллельных прямых и секущей.
      
      В результате поиска доказательства составляется план доказательства теоремы:
      

      План доказательства теоремы.

      ---

      1. Через одну из вершин треугольника провести прямую, параллельную противолежащей стороне.
      2. Доказать равенство внутренних накрест лежащих углов.
      3. Записать сумму внутренних односторонних углов и выразить их через углы треугольника.

      Доказательство и его запись.

      
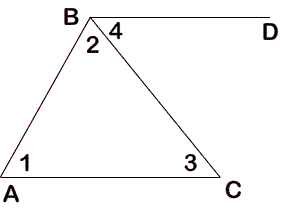
      1. Проведем BD || АС (аксиома параллельных прямых).
      2. ட3 = ட4 (так как это накрест лежащие углы при BD || АС и секущей ВС).
      3. டА + டАВD = 180° (так как это односторонние углы при BD || АС и секущей АВ).
      4. டА + டАВD = ட1 + (ட2 + ட4) = ட1 + ட2 + ட3 = 180°, что и требовалось доказать.

      Закрепление формулировки теоремы и ее доказательства.

      
      
      Для усвоения формулировки теоремы учащимся предлагается выполнить следующие задания:
      1. Сформулируйте теорему, которую мы только что доказали.
      2. Выделите условие и заключение теоремы.
      3. К каким фигурам применима теорема?
      4. Сформулируйте теорему со словами «если …, то…».
3. Применение знаний, формирование умений и навыков.
   1. Решение проблемной задачи. После доказательства теоремы вернемся к задаче, которая явилась мотивацией для изучения теоремы.

      Задача

      ---

      Дано: Треугольник ABC,
      угол A = 50°,
      угол B = 100°,
      Найти: угол C. Решение:
      டA + டB + டC = 180° (по теореме о сумме углов треугольника) ⇒ டC = 180° - (டA + டB) = 180° - (50° + 100°) = 30°.
      Ответ: 30°.
   2. Решение задач по готовым чертежам.

      Найдите неизвестные углы треугольника ABC.

      ---

      
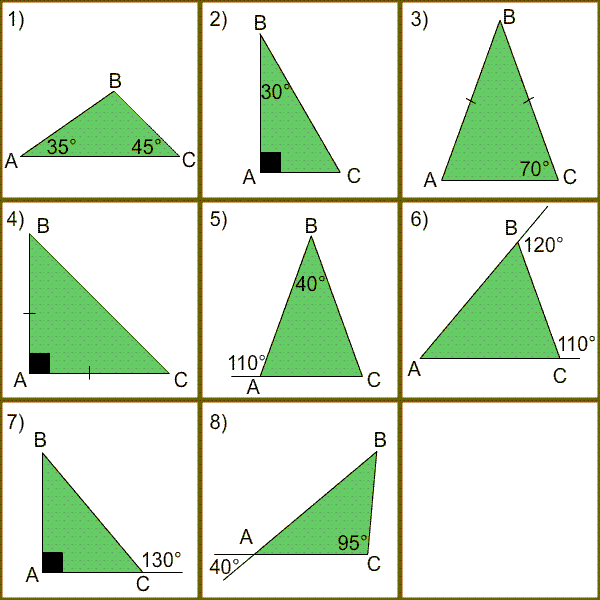
   3. Подведение итогов урока.
      Что нового узнали?
      В чем это новое заключается?
      Где это применяется?
   4. Постановка домашнего задания.

      Домашнее задание.

      ---

      1. Придумайте другие способы доказательства теоремы о сумме углов треугольника, используя следующие чертежи.
      2. § 30, № 223(а), 227(а)
      3. Подготовьте презентацию о развитии учения о треугольниках и об истории доказательства теоремы о сумме углов треугольника (литература: Г. И. Глейзер «История математики в школе 5 — 7 классы») — в течении месяца.